Základným základom všetkých učení, ktoré poznajú svet, je matematika. Presné vedecké využitie formalizovaný jazyk a študuje poradie, štruktúru a vzťahy na vybraných abstraktných objektoch. Nie všetci študenti majú radi matematiku zložitosť a zmätok, ale pravdepodobne preto nedorozumenie. Trvalé zmeny vo vzťahu k matematike si budú vyžadovať obetavosť, koncentráciu, dôslednosť, dokonca tvrdohlavosť a predovšetkým praktické riešenia. V štúdii je dôležité krok za krokom pochopiť spočiatku jednoduchý a postupne prejsť k zložitejšiemu, bez toho, aby zanechali čokoľvek nepochopiteľné a zle pochopené.
Existuje veľa rôznych odvetví matematiky, ktoré boli dostatočne študované a objavili sa nedávno. Ďalej sú popísané základy matematickej analýzy - základné počiatočné pojmy, definície a pravidlá pre štúdium jednoduchých funkcií jednej premennej, derivácie a diferenciácie..
Medzi žiakmi základných škôl došlo k aforizmu: „Matematika sa stáva skutočne komplikovanou, keď z nej zmiznú čísla.“ Skutočne sa približujú k pochopeniu niektorých definícií a zákonov matematickej vedy prostredníctvom rozhodovania o pravidlách pomocou konkrétnych príkladov..
Kľúčové definície
Začnime terminológiou - jednoduchými všeobecnými sémantickými význammi primárnych definícií:
- premenlivý - hodnota alebo symbol, môže mať ľubovoľnú z mnohých hodnôt v
špecifická oblasť (hmotnosť alebo výška dieťaťa)
- funkcie - účel, práca, aktivita, špecifický účinok na premennú, označíme f (x) (závislosť hmotnosti dieťaťa od jeho výšky)
- limit - limit, hranica, hrana (horizont - zorné pole)
- derivát - formovaný, sekundárny, vychádzajúci z iného, označujeme f '(x) (rýchlosť pri pohybe)
- diferenciál - rozdiel, rozlíšenie, oddelenie.
Funkcia je spravodlivá
Funkcia je výsledkom toho, čo robí s premennou, ktorá je výsledok výpočtu. Toto je vzťah prvkov, v ktorých zmena jednej premennej spôsobuje zmenu inej. Rozdeľte písmeno f (x) na jednoduché a zložité.
Nasledujúce metódy sa používajú na zobrazenie závislostí: algebraický, grafický, tabuľkový, logický a dokonca aj softvér.
Numerické závislosti sa určujú algebraicky pomocou symbolov premenných, rovníc a nerovností (≤ a>), zostavuje sa rovnica tvaru: y = f (x), tu x je premenná alebo argument a y alebo f (x) je funkcia. Pre každú špecifickú hodnotu premennej x z prípustnej definičnej oblasti zodpovedá určitá hodnota y pre danú f (x).
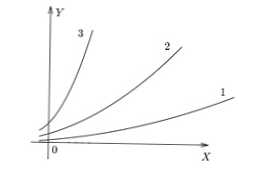
Obrázok nižšie ukazuje jednoduché grafy 3 rôznych pomerov. Je vidieť, že v f (x) 3 je najväčšia hodnota y získaná pre x špecifickú, v f (x) 1 - najmenšia.
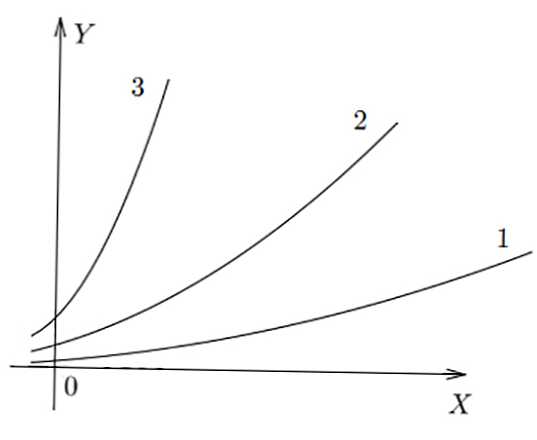
funkcie
Rozlišujú sa tieto základné výrazy: lineárne (priame), kvadratické (parabola), kubické, hyperbola, exponenciálne, logaritmické, trigonometrické (uvedené v tabuľke nižšie).
Pre analýzu každého typu f (x) sa určujú ich základné vlastnosti (uvedené nižšie), na tento účel sa používajú pojmy derivát a diferenciál.
Derivačná funkcia
derivát - operátor, ktoré pre originál f (x) podľa zákonov o diferenciácii priraďuje ďalšiu funkciu, v určitom bode charakterizuje zmenu primárneho f (x) argumentu x. Aby sme to podrobne pochopili, mali by sme sa zaoberať komplexnejšími definíciami hranice závislosti a diferenciácie..
limit - táto definícia je dynamická. Výraz, ktorý má x tendenciu k n, sa chápe nasledovne: x získava hodnoty, ktoré sú blízke n a líšia sa nepatrným množstvom.
diferenciál - malá zmena nejakej veľkosti. Prírastok sa nazýva delta.
Derivát pre f (x) v bode je limit delenia delty funkcie delta premennej v danom bode, ak táto má sklon k 0.
Znak rýchlosti zmeny závislosti v danom bode, geometricky sa môže prejaviť ako hodnota opálenia uhla sklonu alfa dotyčnice k funkcii..
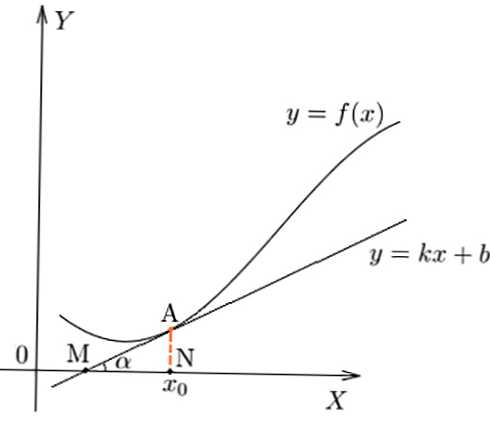
derivát
Závislosť sa nazýva diferencovateľná, ak je definované f '(x). Nájdenie derivátu sa nazýva diferenciácia. Pravidlá výpočtu f '(x) a párovania f' (x) zo elementárneho f (x) sú uvedené v nasledujúcej tabuľke
Odvodená funkcia tiež funguje
Každá závislosť má určité vlastnosti, ich poznanie a skúmanie môžete analyzovať povahu stavu a zmeny f (x).
Hlavné vlastnosti:
- Definícia a údaje o medzerách v hodnote.
- Nula f (x)
- Funkcia sa v niektorých intervaloch zvyšuje alebo znižuje.
- Funkcie bodov MAX a MIN, existuje inflexia.
- Rovnaký alebo nepárny f (x)
- Obmedzená a neobmedzená funkcia.
- Existujú nejaké asymptoty.
- Frekvencia f (x).

Funkcie a deriváty
Pri určovaní charakteristík závislosti pomocou derivátu sa používajú prepojenia vlastností f '(x) s vlastnosťami f (x) a naopak. Charakteristiky f '(x) sa dajú ľahko určiť na funkčnom grafe a naopak, charakteristiky primárneho f (x) sú pochopiteľné z grafu f' (x). Stanovenie podstaty každej funkcie funkcie, vyšetrenie a vytvorenie reťazca vzťahov. Na stanovenie asymptot v grafoch sa používa pojem limitov..
Nižšie sú uvedené niektoré charakteristiky a závislosti f '(x) na f (x):
- Keď sa interval f (x) zvyšuje, f '(x) je pozitívny.
- Ak f (x) klesne v intervale, f '(x) je záporné.
- V prítomnosti f (x) nie je možné určiť bod MAX, f '(x) = 0 a tg dotyčnicového uhla zmení znamienko z + na -.
- V prítomnosti f (x) bod MIN, f '(x) = 0 v ňom nemusí byť stanovený a tg uhla dotyčnice sa mení z - na +.
- Pri ohýbaní f (x) v E hodnota f '(x) nezmenila znamienko v bode, f' (x) = 0.
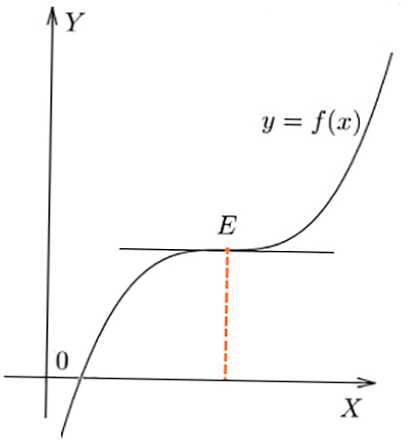
Sklon v bode E funkčného grafu
Pre výskum f (x) tvorí schému, v ktorej je každý krok konštruovaný podľa špecifického algoritmu na výpočet a analýzu vzťahov zložiek prvkov..
Rozdiely vo funkciách a derivátoch
Pravidlá sčítania a odčítania f (x) sú rovnaké ako pravidlá týchto akcií počas diferenciácie. Pravidlá zisťovania f '(x) v rámci akcií násobenia a delenia funkcií sa však líšia (ako v tabuľke)..
Funkcia je primárna a derivát je sekundárna matematická operácia, vo väčšine prípadov majú odlišné charakteristiky.
Inflexný bod súvislej závislosti sa nachádza podľa jeho druhej derivácie, jeho značka by sa mala meniť v oblasti bodu x0.
Existujú také typy funkcií, ktoré nemajú f '(x) v bode x0 (diskontinuálne). Vo výraze ln (| x | -1) derivát nie je definovaný v bode x0 = 1.
Existujú výrazy "Modulo" podobné y = | x |, ktoré má zalomenie v x0.
Pre takéto závislosti sa používajú iba čiastočne (v intervaloch definičnej domény) metódy štúdia ich vlastností pomocou derivátov a nie vždy je možné prejsť z vlastností f '(x) na vlastnosti primárnej.
Nikto nemôže robiť bez výnimiek z pravidiel, dokonca ani z matematiky. Aby bolo možné analyzovať a konsolidovať prezentovaný materiál, je nevyhnutné riešiť príklady, prax, získať skúsenosti s limitmi, diferenciálmi a derivátmi a odvážne prejsť na integrály..











